信息安全
1 密码学基本概念
- 密码系统
- 由明文空间
M、密文空间C、密码方案和密钥空间K组成 - 密码方案
- 加密和解密在密钥
k下运行- 加密
E(m)- encryption => 加密
- message => 明文
m
- 解密
D(c)- decryption => 解密
- ciphertext => 密文
c
- 加密
- 加密和解密在密钥
- 由明文空间
2 密钥分类
1883年Kerchoffs第一次明确提出了编码的原则,即加密算法应建立在算法的公开不影响明文和密钥的安全的基础上。
- 密钥发展史
- 古典密码
- 近现代密码
- 保密性
- 受限制的算法
- 基于密钥的算法
- 加解密密钥是否相同
- 对称密码体制
- 公钥密码体制(非对称密码体制)
- 明文处理方式
- 分组密码算法
- 流密码算法
- 是否可逆的加密变换
- 单向函数密码体制
- 双向变换密码体制
2.1 古典密码
加密思想
- 替代
- 置换
单表替代密码
- 移位密码
- 仿射密码
- 一般单表替代密码
- 密钥短语密码
多表替代密码
- 维吉尼亚密码
- 希尔密码
单表/多表替代密码
- 置换密码
2.1.1 棋盘密码
2.1.1.1 手动计算方法
棋盘密码使用一个5x5的字母方阵对字母进行编码。通常将字母I和J合并到同一个方格中。
例如,使用以下棋盘:
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | A | B | C | D | E |
| 2 | F | G | H | I/J | K |
| 3 | L | M | N | O | P |
| 4 | Q | R | S | T | U |
| 5 | V | W | X | Y | Z |
每个字母由它的行和列表示。例如:
- A -> 11
- B -> 12
- C -> 13
- D -> 14
- E -> 15
- F -> 21
- G -> 22
- H -> 23
- I/J -> 24
- K -> 25
2.1.1.2 示例
加密"HELLO"时:
- H -> 23
- E -> 15
- L -> 31
- L -> 31
- O -> 34
密文为"2315313134"。
2.1.2 移位密码(凯撒密码)
2.1.2.1 手动计算方法
凯撒密码通过将字母表中的每个字母移动固定的位数来加密文本。例如,向右移3位:
- key
- 向右 => +
- 向左 => -
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
- 加密变换:Ek(m)=m+k(mod 26) m∈M, k∈K
- 解密变换:Dk(c)=c-k(mod 26) c∈C, k∈K
2.1.2.2 示例
加密"HELLO"时,移位3位:
- H -> K
- E -> H
- L -> O
- L -> O
- O -> R
密文为"KHOOR"。
2.1.2.3 代码示例
- 加密变换(需要处理两种情况)
import java.util.Scanner;
public class CaesarEncrytion_weak {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.println("输入plaintext");
String plaintext = input.next();
System.out.println("输入key");
int key = input.nextInt();
input.close();
StringBuffer ciphertext = new StringBuffer();
for (int i = 0; i < plaintext.length(); i++) {
char c = plaintext.charAt(i);
// 思路1:a-w(A-W)直接移位加上对应的移位数字
if ((c >= 'a' && c <= 'z' - key) || (c >= 'A' && c <= 'Z' - key)) {
c = (char) (c + key);
} else if ((c >= 'z' - key && c <= 'z') || (c >= 'Z' - key && c <= 'Z')) {
// 思路2:x-z(X-Z) chr-(26-key3) 比如:x x-(26-3)=120-23=97=a
c = (char) (c - (26 - key));
}
ciphertext.append(c);
}
System.out.println("输出ciphertext");
System.out.println(ciphertext);
}
}- 加密变换
import java.util.Scanner;
public class CaesarEncrytion {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.println("输入plaintext");
String plaintext = input.next();
System.out.println("输入key");
int key = input.nextInt();
input.close();
StringBuffer ciphertext = new StringBuffer();
for (int i = 0; i < plaintext.length(); i++) {
char c = plaintext.charAt(i);
if (c >= 'a' && c <= 'z') {
// 验证: (a-97+3)%26+97=3%26+97=3+97=100=d
c = (char) ((c - 'a' + key) % 26 + 'a');
ciphertext.append(c);
} else if (c >= 'A' && c <= 'Z') {
// 验证: (a-97+3)%26+97=3%26+97=3+97=100=d
c = (char) ((c - 'A' + key) % 26 + 'A');
ciphertext.append(c);
}
}
System.out.println("输出ciphertext");
System.out.println(ciphertext);
}
}- 解密变换
import java.util.Scanner;
public class CaesarDecryption {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.println("输入ciphertext");
String ciphertext = input.next();
System.out.println("输入key");
int key = input.nextInt();
input.close();
StringBuffer plaintext = new StringBuffer();
for (int i = 0; i < ciphertext.length(); i++) {
char c = ciphertext.charAt(i);
if (c >= 'a' && c <= 'z') {
// 验证:(d-97-3)%26+97=(100-97-3)%26+97=0%26+97=97=a
c = (char) (Math.floorMod((c - 'a' - key), 26) + 'a');
plaintext.append(c);
} else if (c >= 'A' && c <= 'Z') {
// 验证:(d-97-3)%26+97=(100-97-3)%26+97=0%26+97=97=a
c = (char) (Math.floorMod((c - 'A' - key), 26) + 'A');
plaintext.append(c);
}
}
System.out.println("输出plaintext");
System.out.println(plaintext);
}
}2.1.3 维吉尼亚(Vigenere)密码
2.1.3.1 手动计算方法
- 一种典型的多表替代密码,该密码体制有一个参数
n,表示采用n位长度的字符串(例如一个英文单词)作为密钥。- 设密钥 K = k1, k2, …, kn,明文 M = m1, m2, …, mn
- Ek(m1, m2, …, mn) = (m1 + k1 mod 26, m2 + k2 mod 26 , …, mn + kn mod 26 )
- Dk(c1, c2, …, cn) = (c1 - k1 mod 26, c2 - k2 mod 26 , …, cn - kn mod 26 )
- 循环遍历密钥
K
- 设密钥 K = k1, k2, …, kn,明文 M = m1, m2, …, mn
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
2.1.3.2 示例
- 明文:killthem
- 密钥:gun
- 密钥对应的数字:k = gun = (6, 20, 13)
| 明文 | k | i | l | l | t | h | e | m |
|---|---|---|---|---|---|---|---|---|
| 明文对应数字 | 10 | 8 | 11 | 11 | 19 | 7 | 4 | 12 |
| 密钥 | g | u | n | g | u | n | g | u |
| 密钥对应数字 | 6 | 20 | 13 | 6 | 20 | 13 | 6 | 20 |
| 相加取余 | 16 | 2 | 24 | 17 | 13 | 20 | 10 | 6 |
| 密文 | q | c | y | r | n | u | k | g |
| 密文对应数字 | 16 | 2 | 24 | 17 | 13 | 20 | 10 | 6 |
| 密钥 | g | u | n | g | u | n | g | u |
| 密钥对应数字 | 6 | 20 | 13 | 6 | 20 | 13 | 6 | 20 |
| 相减,负数+26 | 10 | 8 | 11 | 11 | 19 | 7 | 4 | 12 |
| 明文 | k | i | l | l | t | h | e | m |
2.1.4 希尔(Hill)密码
2.1.4.1 手动计算方法
- 希尔密码是一种基于线性代数的密码,它使用矩阵乘法对明文进行加密。密钥是一个方阵,明文被分成向量,与密钥矩阵相乘,然后取模得到密文。
- 数学定义:设m是一个正整数,令M=E=(Z26)m,密钥Km×m={定义在Z26上的m×m矩阵},其中K的行列式值必须和26互素,否则不存在K的逆矩阵K-1。
- 对任意的密钥Km×m
- Ek(m) = Km×m · m (mod 26)
- Dk(c) = K-1m×m · c (mod 26)
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
2.1.4.2 示例
加密矩阵 E
[1 1] [3 4]解密矩阵 D
- D = E-1
- 主对调,负变号
- 二阶矩阵的值 != 0
- 主对角线乘积 - 副对角线乘积 != 0
- 验证
- E = A x (A-1 / |A|) =
[1 0][0 1]
- E = A x (A-1 / |A|) =
[4 -1] [-3 1]- D = E-1
明文 m = "Hill"
明文矩阵 M
[7 11] [8 11]
加密
EM (mod 26) = C => c = "pbwz"
EM = [1 1] [7 11] [3 4] [8 11] = [15 22] [53 77] (mod 26) = C = [15 22] [1 25] = [p w] [b z] = c = "pbwz"
解密
DM (mod 26) = M => m = "hill"
DM = [4 -1] [15 22] [-3 1] [1 25] = [59 63] [-44 -41] (mod 26) = M = [7 11] [8 11] = [h l] [i l] = m = "hill"
2.1.5 仿射密码
2.1.5.1 手动计算方法
- 加密变换
- c = Ek(m) = (k1m + k2) (mod 26)
- 解密变换
- m = Dk(c) = k1-1(c - k2) (mod 26)
- 注意:k1必须和26互素,如果不互素,例如取k1=2,则明文m=mi和m=mi+13两个字符都将被映射成同一个密文字符。
2.1.5.2 示例
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
- 字母表 A - Z
- K1是基本数,假设为3
- K2是加密和解密的移位部分,假设是8
- K3=K1-1是K1的乘法逆元,如果上面是3,这里就是9
- 乘法逆元:如果a和b的乘积模m等于1,那么我们就说b是a模m的乘法逆元
- 数学公式:a x b mod m = 1
- 已知a = 3, m = 26,求b
- 3 x b mod 26 = 1 => b = 9
- 加密
- 明文:ABC
- 对应下标:012
- 计算步骤
- (K1 x M + k2)% 26 = (3 x 0 + 8) % 26 = 8
- (K1 x M + k2)% 26 = (3 x 1 + 8) % 26 = 11
- (K1 x M + k2)% 26 = (3 x 2 + 8) % 26 = 14
- 密文:ILO
- 解密
- K3 x (C - K2) % 26 = 9 x (8 - 8) % 26 = 0
- K3 x (C - K2) % 26 = 9 x (11 - 8) % 26 = 1
- K3 x (C - K2) % 26 = 9 x (14 - 8) % 26 = 2
2.1.5.3 代码示例
import java.util.Scanner;
public class AffineCipher {
// 主函数
public static void main(String[] args) {
// 定义字母表
char[] alphabet = { 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K',
'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W',
'X', 'Y', 'Z' };
// 从用户那里获取明文
Scanner input = new Scanner(System.in);
System.out.println("Please enter the plaintext: ");
String plainText = input.next();
input.close();
// 定义仿射密码的密钥
int k1 = 3;
int k2 = 8;
int k3 = 9;
// 创建 AffineCipher 对象
AffineCipher ac = new AffineCipher();
// 加密明文
String cipherText = ac.encrypt(plainText, alphabet, k1, k2);
// 解密密文
ac.decrypt(cipherText, alphabet, k3, k2);
}
// 加密函数
public String encrypt(String plainText, char[] alphabet, int k1, int k2) {
// 将明文字符串转换为对应的数字数组
int[] plainNum = new int[plainText.length()];
for (int i = 0; i < plainText.length(); i++) {
for (int j = 0; j < alphabet.length; j++) {
if (alphabet[j] == plainText.charAt(i)) {
plainNum[i] = j;
break;
}
}
}
// 使用仿射密码公式进行加密
char[] cipher = new char[plainText.length()];
for (int i = 0; i < plainText.length(); i++) {
int a = Math.floorMod((k1 * plainNum[i] + k2), 26);
cipher[i] = alphabet[a];
}
System.out.println("Encryption: " + new String(cipher));
return new String(cipher);
}
// 解密函数
public String decrypt(String cipherText, char[] alphabet, int k3, int k2) {
// 将密文转换为对应的数字数组
int[] cipherNum = new int[cipherText.length()];
for (int i = 0; i < cipherText.length(); i++) {
for (int j = 0; j < alphabet.length; j++) {
if (alphabet[j] == cipherText.charAt(i)) {
cipherNum[i] = j;
}
}
}
// 使用仿射密码公式进行解密
char[] plainText = new char[cipherText.length()];
for (int i = 0; i < cipherText.length(); i++) {
int a = Math.floorMod((k3 * (cipherNum[i] - k2)), 26);
plainText[i] = alphabet[a];
}
System.out.println("Decryption: " + new String(plainText));
return new String(plainText);
}
}2.1.6 一般单表替代密码
2.1.6.1 手动计算方法
单表替代密码使用一个固定的替代表将字母替换为其他字母。例如,使用以下替代表:
原始字母:A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
替代字母:Q W E R T Y U I O P A S D F G H J K L Z X C V B N M
- 加密
- 遍历明文,如果 = 源字符串 => 密文 += 密码对应字符
- 解密
- 遍历密文,如果 = 密码 => 明文 += 源字符串对应字符
2.1.6.2 示例
加密"HELLO"时:
- H -> I
- E -> T
- L -> S
- L -> S
- O -> G
密文为"ITSSG"。
2.1.6.3 代码示例
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.LinkedHashSet;
import java.util.List;
import java.util.Random;
import java.util.Scanner;
import java.util.Set;
public class SubstitutionAndKeyPhraseCipher {
public static void main(String[] args) {
char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's',
't', 'u', 'v', 'w', 'x', 'y', 'z' };
System.out.println("原始字符数组: " + new String(arr));
Scanner input = new Scanner(System.in);
System.out.println("请输入密钥短语");
// char password[] = initializePassword();
char password[] = initializePassword(input.next());
System.out.println("请输入明文");
String plaintext = input.next();
input.close();
String ciphertext = encrypt(plaintext, arr, password);
System.out.println("加密后: " + ciphertext);
plaintext = decrypt(ciphertext, arr, password);
System.out.println("解密后: " + plaintext);
}
// 密钥短语密码:初始化密码短语
public static char[] initializePassword(String key) {
// 1. 从用户输入的字符串中去除重复字符
Set<Character> chars = new LinkedHashSet<Character>();
for (char c : key.toCharArray()) {
chars.add(c);
}
// 2. 将字符放入数组作为前几个元素
String password = "";
for (char c : chars) {
password += c;
}
// 3. 遍历 'a' 到 'z',检查字符是否已经存在于数组中(contains),
// 如果不存在,则继续追加
for (char c = 'a'; c <= 'z'; c++) {
if (!chars.contains(c)) {
password += c;
}
}
System.out.println("密码短语: " + password);
return password.toCharArray();
}
// 单表替换密码:生成一个从 'a' 到 'z' 的随机字符数组
public static char[] initializePassword() {
List<Character> chars = new ArrayList<Character>();
for (char c = 'a'; c <= 'z'; c++) {
chars.add(c);
}
Collections.shuffle(chars, new Random());
String password = "";
for (char c : chars) {
password += c;
}
System.out.println("密码短语: " + password);
return password.toCharArray()
}
// 加密方法
public static String encrypt(String plaintext, char arr[], char password[]) {
String ciphertext = ""; // 初始化密文字符串
for (int i = 0; i < plaintext.length(); i++) { // 遍历明文中的每个字符
char c = plaintext.charAt(i); // 获取当前字符
for (int j = 0; j < arr.length; j++) { // 遍历字符数组
if (c == arr[j]) { // 如果当前字符等于字符数组中的某个字符
ciphertext += password[j]; // 将对应的密钥字符添加到密文字符串
break; // 跳出内层循环
}
}
}
return ciphertext; // 返回密文字符串
}
// 解密方法
public static String decrypt(String ciphertext, char arr[], char password[]) {
String plaintext = ""; // 初始化明文字符串
for (int i = 0; i < ciphertext.length(); i++) { // 遍历密文中的每个字符
char c = ciphertext.charAt(i); // 获取当前字符
for (int j = 0; j < password.length; j++) { // 遍历密钥数组
if (c == password[j]) { // 如果当前字符等于密钥数组中的某个字符
plaintext += arr[j]; // 将对应的字符数组字符添加到明文字符串
break; // 跳出内层循环
}
}
}
return plaintext; // 返回明文字符串
}
}2.1.7 密钥短语密码
2.1.7.1 手动计算方法
密钥短语密码使用一个关键词生成替代表。关键词中的字母在表前,剩下的字母按字母顺序排列。
关键词为"KEYWORD":
- 去重后:KEYWORD
- 剩余字母:A B C F G H I J L M N P Q S T U V X Z
生成的替代表:
K E Y W O R D A B C F G H I J L M N P Q S T U V X Z
- 加密
- 遍历明文,如果 = 源字符串 => 密文 += 密码对应字符
- 解密
- 遍历密文,如果 = 密码 => 明文 += 源字符串对应字符
2.1.7.2 示例
加密"HELLO"时:
- H -> I
- E -> E
- L -> J
- L -> J
- O -> R
密文为"IEJJR"。
2.1.7.3 代码示例
import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.LinkedHashSet;
import java.util.List;
import java.util.Random;
import java.util.Scanner;
import java.util.Set;
public class SubstitutionAndKeyPhraseCipher {
public static void main(String[] args) {
char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's',
't', 'u', 'v', 'w', 'x', 'y', 'z' };
System.out.println("原始字符数组: " + new String(arr));
Scanner input = new Scanner(System.in);
System.out.println("请输入密钥短语");
// char password[] = initializePassword();
char password[] = initializePassword(input.next());
System.out.println("请输入明文");
String plaintext = input.next();
input.close();
String ciphertext = encrypt(plaintext, arr, password);
System.out.println("加密后: " + ciphertext);
plaintext = decrypt(ciphertext, arr, password);
System.out.println("解密后: " + plaintext);
}
// 密钥短语密码:初始化密码短语
public static char[] initializePassword(String key) {
// 1. 从用户输入的字符串中去除重复字符
Set<Character> chars = new LinkedHashSet<Character>();
for (char c : key.toCharArray()) {
chars.add(c);
}
// 2. 将字符放入数组作为前几个元素
String password = "";
for (char c : chars) {
password += c;
}
// 3. 遍历 'a' 到 'z',检查字符是否已经存在于数组中(contains),
// 如果不存在,则继续追加
for (char c = 'a'; c <= 'z'; c++) {
if (!chars.contains(c)) {
password += c;
}
}
System.out.println("密码短语: " + password);
return password.toCharArray();
}
// 单表替换密码:生成一个从 'a' 到 'z' 的随机字符数组
public static char[] initializePassword() {
List<Character> chars = new ArrayList<Character>();
for (char c = 'a'; c <= 'z'; c++) {
chars.add(c);
}
Collections.shuffle(chars, new Random());
String password = "";
for (char c : chars) {
password += c;
}
System.out.println("密码短语: " + password);
return password.toCharArray()
}
// 加密方法
public static String encrypt(String plaintext, char arr[], char password[]) {
String ciphertext = ""; // 初始化密文字符串
for (int i = 0; i < plaintext.length(); i++) { // 遍历明文中的每个字符
char c = plaintext.charAt(i); // 获取当前字符
for (int j = 0; j < arr.length; j++) { // 遍历字符数组
if (c == arr[j]) { // 如果当前字符等于字符数组中的某个字符
ciphertext += password[j]; // 将对应的密钥字符添加到密文字符串
break; // 跳出内层循环
}
}
}
return ciphertext; // 返回密文字符串
}
// 解密方法
public static String decrypt(String ciphertext, char arr[], char password[]) {
String plaintext = ""; // 初始化明文字符串
for (int i = 0; i < ciphertext.length(); i++) { // 遍历密文中的每个字符
char c = ciphertext.charAt(i); // 获取当前字符
for (int j = 0; j < password.length; j++) { // 遍历密钥数组
if (c == password[j]) { // 如果当前字符等于密钥数组中的某个字符
plaintext += arr[j]; // 将对应的字符数组字符添加到明文字符串
break; // 跳出内层循环
}
}
}
return plaintext; // 返回明文字符串
}
}2.1.8 置换密码
2.1.8.1 手动计算方法
置换密码通过重新排列明文中的字符位置来加密信息。这里使用栅栏式置换。在栅栏式置换中,明文被写成栅栏形状的多个行,然后按行读取密文。
假设密钥为N,那么明文将分为N行。字符按从上到下、再从下到上的锯齿形方式排列,直到结束。然后按行读取字符,组成密文。
2.2 密钥分配
- 解决密钥分配问题的关键
- 线路上传输的必须是公钥
- 这个公钥必须是接收方的
如果A/B双方需要使用公钥加密算法互相发送加密信息,则需要两对公/私钥。即使用对方公钥进行加密。
要防止接收方的公钥被假冒。
对称密码系统需要的密钥数
密钥数与参与通信人数的平方成正比
公钥密码系统需要的密钥数
n人 =>n对
| 特征 | 对称密钥加密 | 公钥加密 |
|---|---|---|
| 加/解密所用密钥 | 相同 | 不同 |
| 加/解密速度 | 快 | 慢 |
| 密文长度 | 通常等于或小于明文长度 | 大于明文长度 |
| 密钥分配 | 大问题 | 没问题 |
| 系统所需密钥总数 | 大约为参与者的平方个 | 等于参与者的个数 |
| 用法 | 主要用于加/解密 (作会话密钥) | 主要用于加密会话密钥,数字签名 |
| 密钥产生方式 | 集中式 | 分散式 |
|---|---|---|
| 代表 | 密钥分配中心/CA证书分发中心 | 个人产生 |
| 生产者 | 在中心统一进行 | 用户 |
| 用户数量 | 用户数量受限制 | 用户数量不受限制 |
| 特点 | 密钥质量高,方便备份 | 需第三方认证 |
| 安全性 | 需安全的私钥传输通道 | 安全性高,只需将公钥传送给CA |
2.2.1 对称密码体制
NOTE
加密密钥与解密密钥相同,这种体制只要知道加/解密算法,就可以反推解/加密算法。
在1976年公钥密码算法提出以前的所有加密算法都是对称密码体制。
对称密码体制
- 分组密码
- 分组密码将明文分成固定大小的块,然后使用相同的加密算法对每个块进行加密。
- AES
- 目前最流行的分组密码之一,用于各种应用,包括无线网络安全、文件加密和电子商务。
- DES
- 曾是美国政府的标准加密算法,但现在已被 AES 取代
- Blowfish
- 免费且不受专利限制。
- AES
- 分组密码将明文分成固定大小的块,然后使用相同的加密算法对每个块进行加密。
- 流密码
- 流密码将明文和密钥流逐位异或(XOR)以生成密文。密钥流通常是使用伪随机数生成器(PRNG)从种子密钥生成的。
- RC4
- 现在已被认为不安全,不应再使用。
- A5/1
- 由 GSM(全球移动通信系统)使用。已被破解,不应再用于安全通信。
- ChaCha20
- ChaCha20 是一种快速且安全的流密码算法,适用于各种应用。
- RC4
- 流密码将明文和密钥流逐位异或(XOR)以生成密文。密钥流通常是使用伪随机数生成器(PRNG)从种子密钥生成的。
- 分组密码
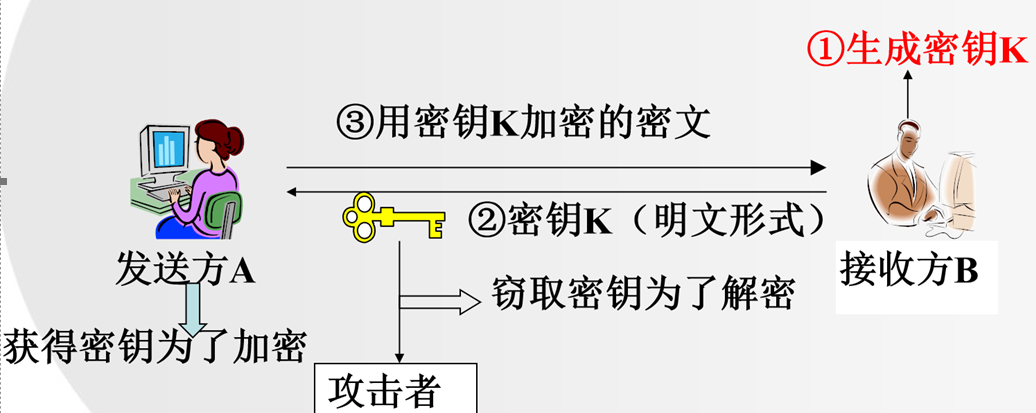
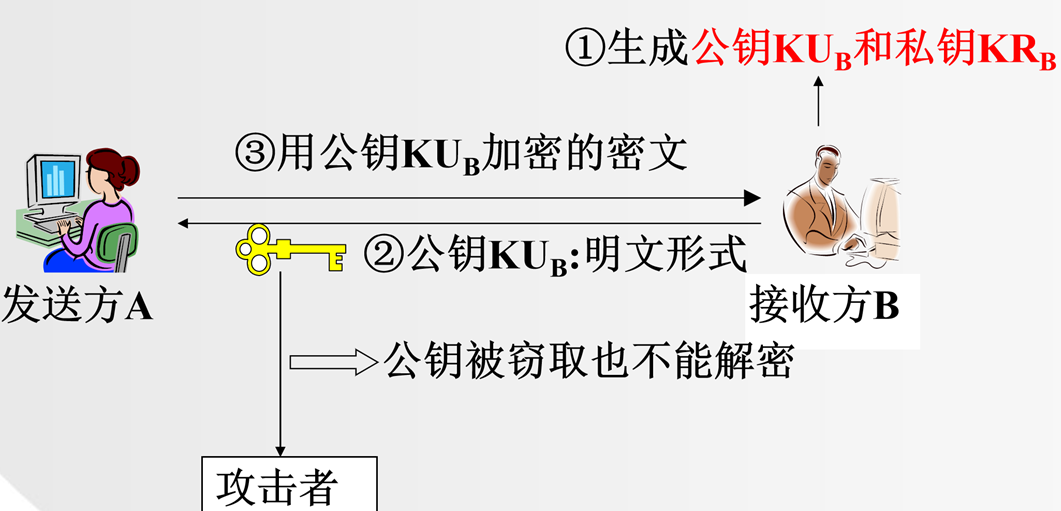
2.2.2 公钥密码体制
加密使用公钥公开,无法实现保密性
NOTE
- 公钥密码体制
- DSA(Digital Signature Algorithm)
- 基于椭圆曲线密码学的公钥密码体制。它通常用于数字签名,因为与RSA相比,DSA的签名生成和验证速度更快。
- ECC(Elliptic Curve Cryptography)
- 基于椭圆曲线数学的公钥密码体制。它与RSA一样,也用于加密和解密数据。ECC的优势在于它可以在较短的密钥长度下提供同等的安全性。
- Paillier加密
- 同态加密方案,密文可以进行某些计算操作,而无需解密。数据可以加密存储在云端,而无需担心数据泄露,适合于云计算等应用。
- RSA
- 密钥长度过长,性能开销大。
- 存在潜在的量子攻击漏洞。
- 公钥和私钥通常分别用
KU和KR来指定。这是一种约定,并没有严格的技术规定。 KU代表 Key Usage,即公钥的使用用途:- 加密数据
- 验证数字签名
- 进行密钥交换
KR代表 Key Role,即私钥的角色:- 解密由公钥加密的数据
- 生成数字签名
- 进行密钥交换
3 数字签名
3.1 数字签名基本原理
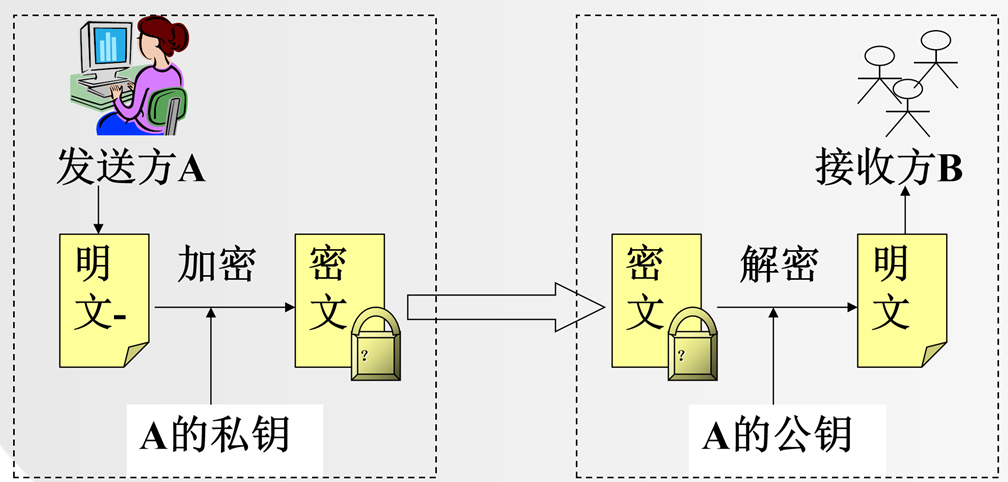
3.2 数字签名作用
- 实现消息认证
- 证实某个消息确实是某用户发出的。
- 签名不可伪造(特点)
- 收方和第三方都不能伪造签名(unforgeable)
- 签名不可重用(特点)
- 签名是消息(文件)的一部分(绑定在一起),不能把签名移到其它消息(文件)上
- 实现不可抵赖性
- 消息的发送方不能否认他曾经发过该消息。
- 完整性保证
- 如果消息能够用公钥解密成功,还可确信消息在传输过程中没有被篡改过。
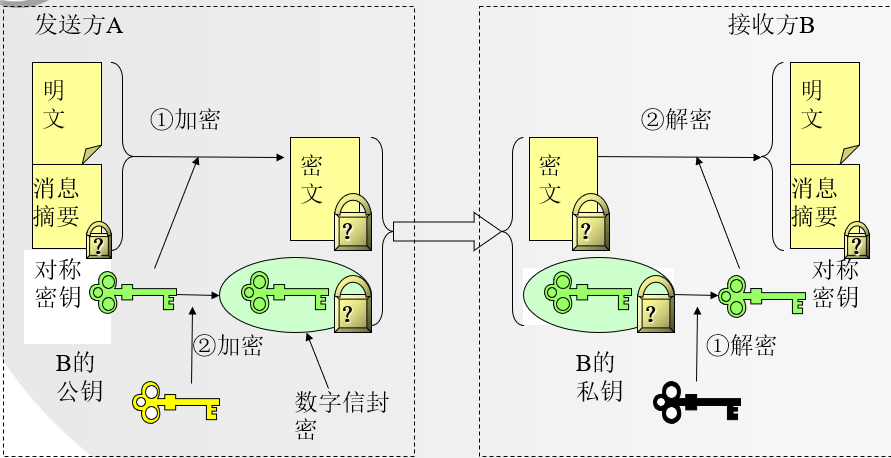
3.3 数字信封
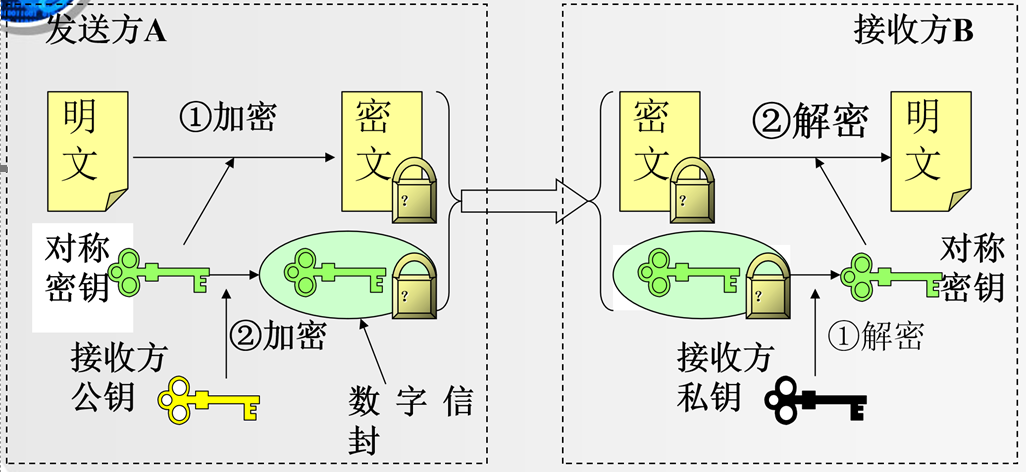
不可逆加密体制
单向散列函数 => 不可逆加密体制(单向密码体制)
用于口令验证等场景(把登录密码加密后和已加密的数据库对应密码比较)
3.4 数字签名过程
3.4.1 数字签名基本过程
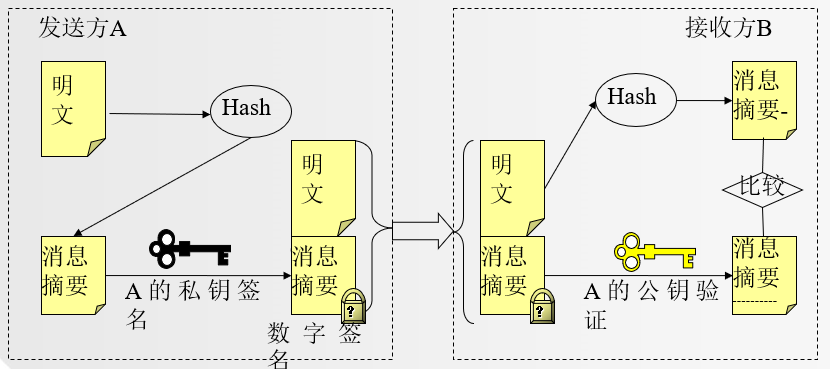
3.4.2 带有保密性的数字签名过程
4 散列函数 (HASH)
散列函数(Hash Functions)是将任意长度的输入数据(称为消息)转换为固定长度的输出数据(称为哈希值或摘要)的算法。这些函数在计算机科学中具有广泛的应用,例如数据校验、数字签名、哈希表和密码学。散列函数具有以下几个重要特性:
- 确定性:相同的输入总是生成相同的输出。
- 快速计算:对任意输入数据都能迅速计算出其哈希值。
- 雪崩效应:输入的微小变化会导致输出的哈希值有显著变化。
- 抗碰撞性:很难找到两个不同的输入具有相同的哈希值(称为碰撞)。
- 单向性:从哈希值几乎不可能反推出原始输入。
4.1 常用的散列函数
MD5(Message-Digest Algorithm 5):
- MD5 由 Ronald Rivest 于1991年设计。
- 生成128位(16字节)的哈希值。
- 尽管曾广泛使用,但由于存在严重的安全漏洞(如碰撞攻击),现在不推荐用于安全敏感的场合。
SHA-1(Secure Hash Algorithm 1):
- 由美国国家安全局(NSA)设计,并由NIST发布。
- 生成160位(20字节)的哈希值。
- 同样由于碰撞漏洞问题,已被认为不安全,目前逐渐被淘汰。
SHA-2(Secure Hash Algorithm 2):
- 包含多个变种,如SHA-224、SHA-256、SHA-384和SHA-512,分别生成224位、256位、384位和512位的哈希值。
- 由NSA设计,是SHA-1的继任者,目前仍然广泛使用并被认为是安全的。
SHA-3(Secure Hash Algorithm 3):
- 基于Keccak算法,由Guido Bertoni、Joan Daemen、Michaël Peeters和Gilles Van Assche设计。
- 包括SHA3-224、SHA3-256、SHA3-384和SHA3-512变种。
- 是SHA-2的替代方案,提供了与SHA-2不同的算法结构,增强了多样性。
RIPEMD-160:
- 由Hans Dobbertin、Antoon Bosselaers和Bart Preneel设计。
- 生成160位的哈希值。
- 虽然没有SHA-2和SHA-3那么广泛使用,但在某些应用中仍然可见。
CRC32(Cyclic Redundancy Check 32):
- 一种非加密散列函数,主要用于检测数据传输或存储中的错误。
- 生成32位的校验值。
Blake2:
- 由Jean-Philippe Aumasson等人设计。
- 比SHA-2更快,并且在安全性和效能之间提供了很好的平衡。
- 生成可变长度的哈希值(如Blake2b生成512位,Blake2s生成256位)。
MurmurHash:
- 由Austin Appleby设计,适用于哈希表等应用的非加密散列函数。
- 快速且具有很好的散列分布特性,常用于内存和性能要求较高的场景。
CityHash:
- 由Google开发,设计用于高效地对大字符串进行哈希计算。
- 提供不同的版本(如CityHash64、CityHash128),以适应不同的性能需求。
4.2 MAC
在密码学中,MAC(Message Authentication Code,消息认证码)是一种用于验证消息完整性和真实性的技术,它类似于散列函数,但使用了密钥来增加安全性。MAC 在消息传递过程中可以防止数据被篡改或伪造。
MAC 通常使用散列函数和密钥来生成一个固定长度的密文,这个密文被称为消息认证码。发送方使用密钥对消息进行加密,然后将消息和生成的 MAC 一起发送给接收方。接收方使用相同的密钥对接收到的消息进行解密,并计算消息的 MAC,然后比对计算得到的 MAC 和接收到的 MAC 来验证消息的完整性和真实性。
常见的 MAC 算法包括 HMAC(基于哈希的消息认证码)和 CMAC(密码消息认证码)等。MAC 在网络通信、数据传输和身份验证等领域被广泛应用,是保证通信安全性的重要技术之一。